BME280 Absolute Temperature Accuracy
Introduction
In all my hygrometer calibration write-ups to date I plotted the temperature data but always stated it was only a relative comparison between the various sensors. I do not have a traceable calibrated thermometer or other absolute reference to say if the temperatures were 'correct'. I could only say 'they all agree'. After seeing several reports on the internet of BME280s reading up to 5°C high, I have attempted an absolute calibration check. This is only a single point test since the only reference I have is the ice point of water at 0°C.
The BME280 datasheet is clear that this device is not designed to be a precision thermometer but the hearsay about large errors made me want to look closer.
Method
More modern international standards (e.g. ITPS-68, ITS-90) have replaced this definition, but to within the precision I can hope to achieve, the definition of 0°C is simply the ice point of water. Though that sounds simple, I had previously assumed subtle complications would limit the usefulness of an ice bath test without access to lab grade facilities. After reading NIST Technical Note 1411, 'Reproducibility of the temperature of the ice point in routine measurements' (B.W. Mangum, 1995), I became more confident that it is a usable method. That document contains a detailed procedure for producing an ice bath and then demonstrates how, following the rather simple methodolgy, consistency of ±0.002°C is routinely maintained over many years. My aspiration in this test is only ±0.1°C.
NIST Technical Note 1411 says 'A properly prepared ice bath is one that consists of a cylindrical Dewar flask (a typical size is one that is approximately 8 cm in diameter and 36 cm deep), a siphon tube, shaved ice prepared from distilled water, and distilled water that just fills the voids between the ice particles but does not float the ice. The siphon tube should extend to the bottom of the Dewar for ease in removing the excess water produced by the melting of the ice. In preparing the ice bath, the Dewar flask should be filled to approximately one-third of its capacity with air-saturated distilled water and then the shaved or crushed ice should be added until the flask is full.' Read the original document for the full procedure. Any large vacuum (e.g., 'Thermos™') flask is a suitable Dewar after thorough cleaning and a long straw is sufficient for the siphon tube. I used distilled water from the supermarket which may not be of the highest purity, but in the above cited document they note that for many years NIST used commerically produced ice, not distilled at all and tests deliberately performed with tap water were consistent with those from ultra-pure water within the ±0.002°C repeatability. I live at over 5000' altitude which does change the ice point, but I estimate only by 0.001°C and I have made no compensation in my measurements. I had initially planned to boil the distilled water to drive off dissolved gases, but was surprised to note in the instructions above they specify 'air-saturated distilled water' which makes life much easier. In any case, my calculations based on Henry's Law for the solubility of gasses and Blagden's Law for freezing point depression give me the molar concentration of air in water as less than 1×10-3 and a maximum implied error of 0.001°C. In summary, I see no reason why ±0.1°C should not be achievable with a little care.
I cannot immerse the BME280 directly in the ice bath. Instead I used three waterproof encapsulated DS18B20s. I averaged the readings for twelve hours producing a zero point calibration for each device. They were then removed from the ice bath, dried and I logged the air temperature from all three along with the BME280. From the difference between the BME280 and the DS18B20, along with the DS18B20 zero point, I can determine the absolute accuracy of the device being assessed. Using three DS18B20s provides a consiency check. A fan provided a continuous, gentle airflow over the sensors throughout the test. Values were averaged over several hours and though the air temperature drifted between −2 and +1°C, the offset between devices was stable to an RMS of <0.02°C. Note that I was fortunate that the air temperature happened to be very close to zero so scale errors in the DS18B20 are no concern. I am testing at very close to the calibration point (0°C). In Summer, it might be best to operate in the fridge though domestic fridges tend to cycle temperature quite rapidly which could cause more problems than it solves.
Results
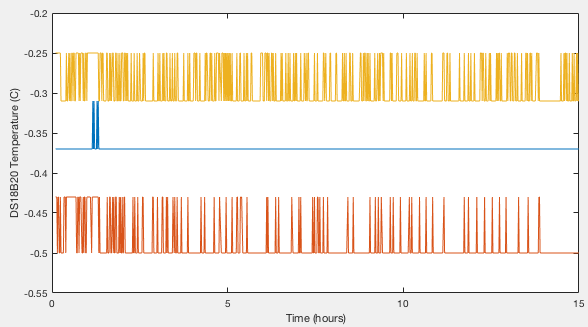
Zero point calibration of DS18B20
Three devices (S.N. 28:FF:8F:39:A1:15:04:18, 28:FF:5E:39:A1:15:03:08, 28:FF:93:4C:A1:15:03:EF) were immersed in the ice bath, logging readings once per minute for 802 minutes. Results are shown in Figure 1. The best resolution of the DS18B20 is 0.06°C, giving highly quantised data. We can average over time and derive a mean temperature with a standard error of <0.001°C, however without understanding a lot more about how the DS18B20 internally handles analogue-to-digital conversion and rounding, the best error I am willing to quote is half the native resolution, or 0.03°C. (We will revisit this very conservatively estimated error later and show that we can in reality do rather better.) The three devices thus have zero points of −0.369, −0.488 and −0.291 ±0.03°C.
The BME280 devices
Six devices have been tested. Two (labelled 'M' and 'N' in my logs) were included in the previous humidity tests. Four (labelled 'Q', 'R', 'S', 'T') are new and not previously tested. Each was monitored for at least eight hours. Results from device 'M' are shown in Figure 2. Though the temperature drifts with time, the offset between any given pair of sensors remains constant within an RMS of 0.002°C, even when I physically disturbed the apparatus at around 11hours. After applying the ice bath zero points, the absolute error for this sensor is +0.29, +0.29 and +0.27 °C as determined with respect to the three reference DS18B20s. The values agree within the stated zero point error of ±0.03°C. Figures 11 and 12 of my humidity calibration study show this device had a relative offset from the ensemble average of all my devices of around +0.3°C showing that the set ensemble average turns out to have been a pretty good absolute calibration.
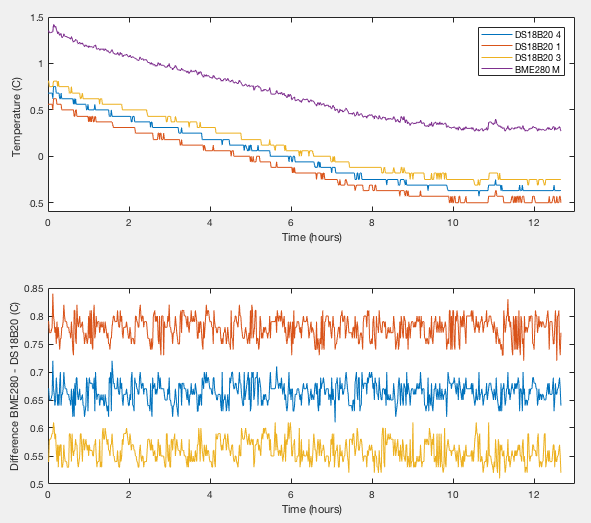
| Tdiff between BME280 and DS18B20 (°C) | BME280 zero point from each reference (°C) | |||||
| DS18B20 4 | DS18B20 1 | DS18B20 3 | DS18B20 4 | DS18B20 1 | DS18B20 3 | |
| BME280 M | +0.664±0.02 | +0.779±0.02 | +0.559±0.02 | +0.29 | +0.29 | +0.27 |
| BME280 Q | +0.258±0.02 | +0.400±0.02 | +0.186±0.02 | −0.11 | −0.09 | −0.10 |
| BME280 N | +1.058±0.02 | +1.177±0.02 | +0.960±0.02 | +0.69 | +0.69 | +0.67 |
| BME280 R | +0.590±0.02 | +0.693±0.02 | +0.487±0.02 | +0.22 | +0.20 | +0.20 |
| BME280 S | +0.357±0.02 | +0.458±0.02 | +0.260±0.02 | −0.01 | −0.03 | −0.03 |
| BME280 T | −0.159±0.02 | −0.060±0.02 | −0.274±0.02 | −0.53 | −0.55 | −0.56 |
We can now revisit the estimate on the ice bath measurement precision by comparing the DS18B20 values to the ensemble average of a sample of six BME280s. This argument becomes dangerously circular with each device being compared mutually against the other. We therefore lose the absolute calibration which was the point of using the ice bath, but it does allow us to expose systematic offsets between the three DS18B20 zero points. There are none. Comparing each DS18B20 in turn to the average of all the BME280s shows instrumental errors in our DB18B20 zero points of less than 0.01°C. There could still be fundamental problems with the ice bath that affects all three devices equally, but we have shown that long term averaging of the quantised DS18B20 data to give a precision much finer than the natively reported resolution is valid. Excluding systematic errors induced by the ice bath itself, empirically determined instrumental errors on the DS18B20 zero points are only ±0.01°C compared with my a priori ±0.03°C estimate.
Finally, I returned the DS18B20s to the ice bath again to check consistency over the intervening week. I get −0.370, −0.488 and −0.284°C. The largest change is +0.007°C for sensor 3, again confirming the assertion that measurement errors are smaller than 0.01°C.
| Device | Zero Point (°C) |
| DS18B20 4 | −0.37±0.01 |
| DS18B20 1 | −0.49±0.01 |
| DS18B20 3 | −0.29±0.01 |
| BME280 M | +0.283±0.02 |
| BME280 Q | −0.100±0.02 |
| BME280 N | +0.683±0.02 |
| BME280 R | +0.207±0.02 |
| BME280 S | −0.025±0.02 |
| BME280 T | −0.547±0.02 |
Discussion
All the devices I have tested so far have been within specification and I see no large deviations like those reported by other users. This is only a one point calibration at 0°C. The good agreement between measurements here and the previously presented relative tests for sensors M and N shows that they were in fact fairly good representations of absolute accuaracy, at least at 0°C and within a precision of a couple of tenths of a degree. In other words, the error on the ensemble average was close to zero.
So what is going wrong in those other cases? It could be defective devices, non-OEM fake clones or user error. Self-heating is a possibility, but should not account for more than 0.5°C and some correspondents confirm they have slowed down the internal sampling rate and still see high temperatures. One idea someone suggested was the possibility of low-quality voltage regulators built into 5V tolerant modules disturbing the sensor. I am running mine at 3.3V so cannot comment. Another idea suggested to me was manufacturers of cheap integrated modules not having followed the Bosch Sensortec soldering profile properly and contaminated or damaged the device. The reconditioning procedure might resolve that. (Both soldering profile and reconditioning procedure can be found in the datasheet.) That is a long list of suggestions I have heard, but all I can say is that all those I have bought and tested have been good.
If you have comments or suggestions feel free to contact me:
2018-02-25 4:27 PM